Analysis and Simulation of Current Sources

Table of Contents

1. Background
2. JFET
   1. Circuit Overview
   2. Design
   3. Example Calculation
   4. SPICE Model Usage
   5. Example Calculation
   6. Sensitivity
   7. Simulation
3. Howland Current Source
   1. Circuit Overview
   2. Analysis
   3. Sensitivity Analysis
4. Design Considerations
   1. Limitations
      1. Supply Limits
      2. Current Limit
      3. Resistor Trimming
      4. Thermal Management and Quiescent Power Usage
   2. Compliance Limit
      1. Additional Considerations
   3. Component Value Calculation
5. Summary
6. Definitions
7. References
8. Table of Figures
9. Table of Equations

Background

Figure 1 - LTSpice Simulation Schematic

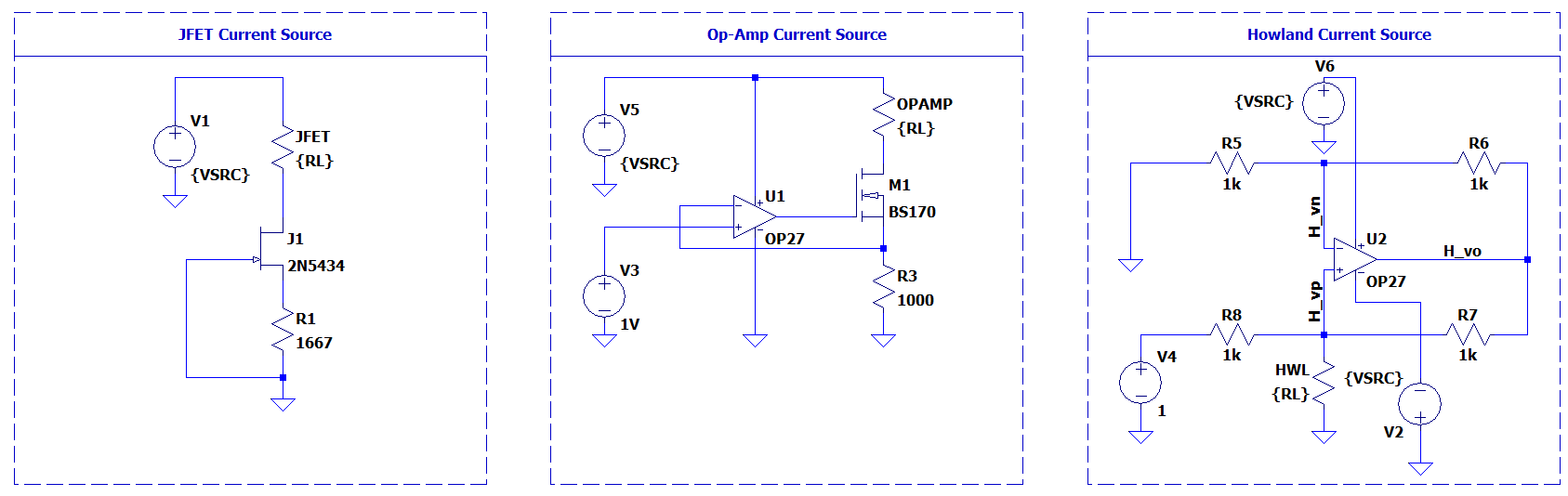
Current sources are a fundamental source in electronics. They are used to generate a precise current that can be applied to a system. This system is often sensors or other measurement application where the known current is used to generate a voltage which can be processed by an analog to digital converter to a digital value. This value can then be acted upon, or logged for instance. Ultimately their uses are numerous and not limited to only digital systems. They come in many forms from nano-amp current mirrors in semiconductors to kiloamps in an industrial process for plating or electrochemical cells.

An ideal current source has an infinite compliance voltage, zero output impedance and does not have dependence on the supplied voltage. In reality all of these factors limit the performance of a current source.

There are many different kinds of current sources. In this article the JFET and Howland architectures are discussed that have applications primarily within PCBA level designs. A simple op-amp-FET circuit is added to the simulation for comparison.

JFET

Figure 2 - JFET Semiconductor Structure

The JFET current source is one of the simplest to implement. It consists of a Junction Field Effect Transistor (JFET) and a resistor. These can also be purchased in a standalone package known as a constant current diode.

Circuit Overview

Design

The design of a JFET constant current source primarily depends on two datasheet parameters: $V_{GS(off)}$ and $I_{DSS}$. The resistor value is chosen to create the proper voltage drop, causing the JFET to conduct only the specified current.

\[\Large V_{GS} = -V_{GS(off)} \cdot \left( 1-\sqrt{\frac{I_D}{I_{DSS}}} \right)\] Equation 1 - JFET Gate Source Voltage

The required resistance can then be calculated using Ohm’s law.

\[\Large R_{DS} = \frac{V_{GS}}{I_D}\] Equation 2 - JFET Drain Resistance

Example Calculation

Parameter	Value	Units
$V_{GS(off)}$	-1.90	V
$I_D$	1.0e-3	A
$I_{DSS}$	64.90e-3	A

\[\Large V_{GS} = -(-1.90V) \cdot \left( 1-\sqrt{\frac{1\mathrm{e}{-3} A}{64.90e-3 A}} \right) =1.664V\] \[\Large R_{DS} = \frac{1.664V}{1.0\mathrm{e}{-3}} = 1664 \Omega\]

SPICE Model Usage

Component parameters can also be determined using SPICE models when datasheet values are unavailable or inconsistent. For instance the following is a model of the 2N5434 JFET. The resistor can be determined using these model parameters to match the desired current.

Note that the SPICE model parameters are typically nominal values and may not be representative of the extremes.

.model 2N5434 NJF(Beta=18m Betatce=-.5 Rd=1 Rs=1 Lambda=25m Vto=-1.9 Vtotc=-2.5m Is=.5p Isr=5p Alpha=150u Vk=110 Cgd=35p M=.4283 Cgs=35p mfg=Vishay)

\[\Large I_D = \beta (V_{GS} - V_{TO})^2\] Equation 3 - Drain Current \[\Large \textcolor{WildStrawberry}{I_{DSS}} = \textcolor{Cerulean}{\beta} \cdot \textcolor{BurntOrange}{V_{TO}}^2\] Equation 4 - Drain Saturation

where:

• $\beta$ is the transconductance parameter ($A/V^2$).
• $V_{GS}$ is the gate-source voltage.
• $V_{TO}$ is the pinch-off voltage.
• $I_D$ is the drain current.
• $I_{DSS}$ is the drain saturation current (The value of $I_D$ with $V_{GS}=0$).

Example Calculation

Using the SPICE model, the resistor can be determined as follows for a $1mA$ constant current source:

\[\Large \textcolor{WildStrawberry}{I_{DSS}} = \textcolor{Cerulean}{(0.018A/V^2)} \cdot \textcolor{BurntOrange}{(-1.9)}^2 = \textcolor{WildStrawberry}{0.06498 A}\] \[\Large V_{GS} = -(-1.90V) \cdot \left( 1-\sqrt{\frac{1\mathrm{e}{-3} A}{64.98\mathrm{e}{-3} A}} \right) =1.664V\] \[\Large R = \frac{V}{I} = \frac{1.664V}{0.001A} = 1664 \Omega\]

Sensitivity

Figure 3 - JFET Load Resistance Sensitivity Plot

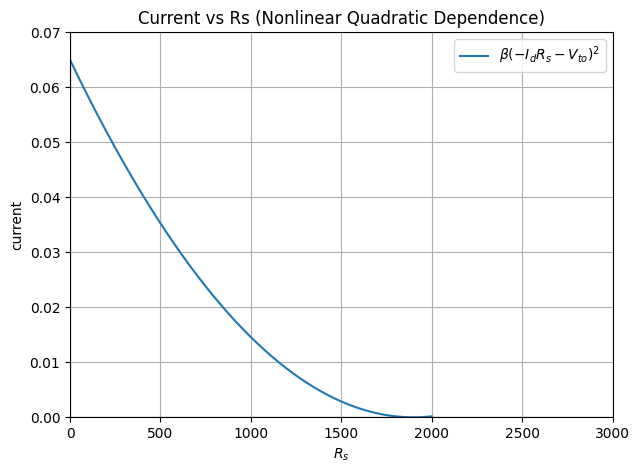
The variance due to the resistance tolerance can be calculated by rearranging the drain current equation by substituting voltage for the resistance and current. The effects of resistance change are nonlinear in nature as can be visualized on the chart.

\[\Large I_D = \beta (V_{GS} - V_{TO})^2 = \beta (-I_D \cdot R_s-V_{TO})^2\] Equation 5 - JFET Drain Current \[\Large \frac{\partial I_D}{R_s} = 2 I_{d} \beta \left(I_{D} R_{s} + V_{TO}\right)\] Equation 6 - JFET Drain Current vs Load Resistance Derivative

Simulation

Figure 4 - JFET Simulation Circuit

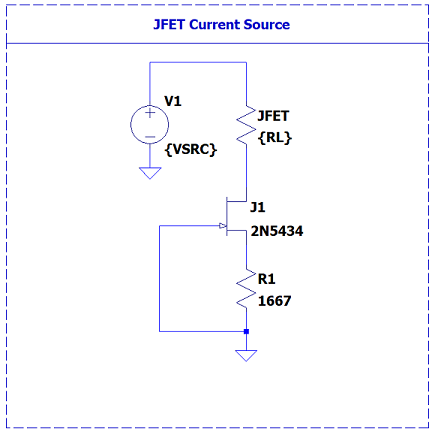
The JFET circuit was simulated in LTspice. It is relatively stable with changes in supply voltage but varies slightly due to channel-length modulation. ¹ This channel length modulation effect is shown as an increasing curve with applied voltage.

Figure 5 - JFET Simulation Results, Current vs Applied Voltage

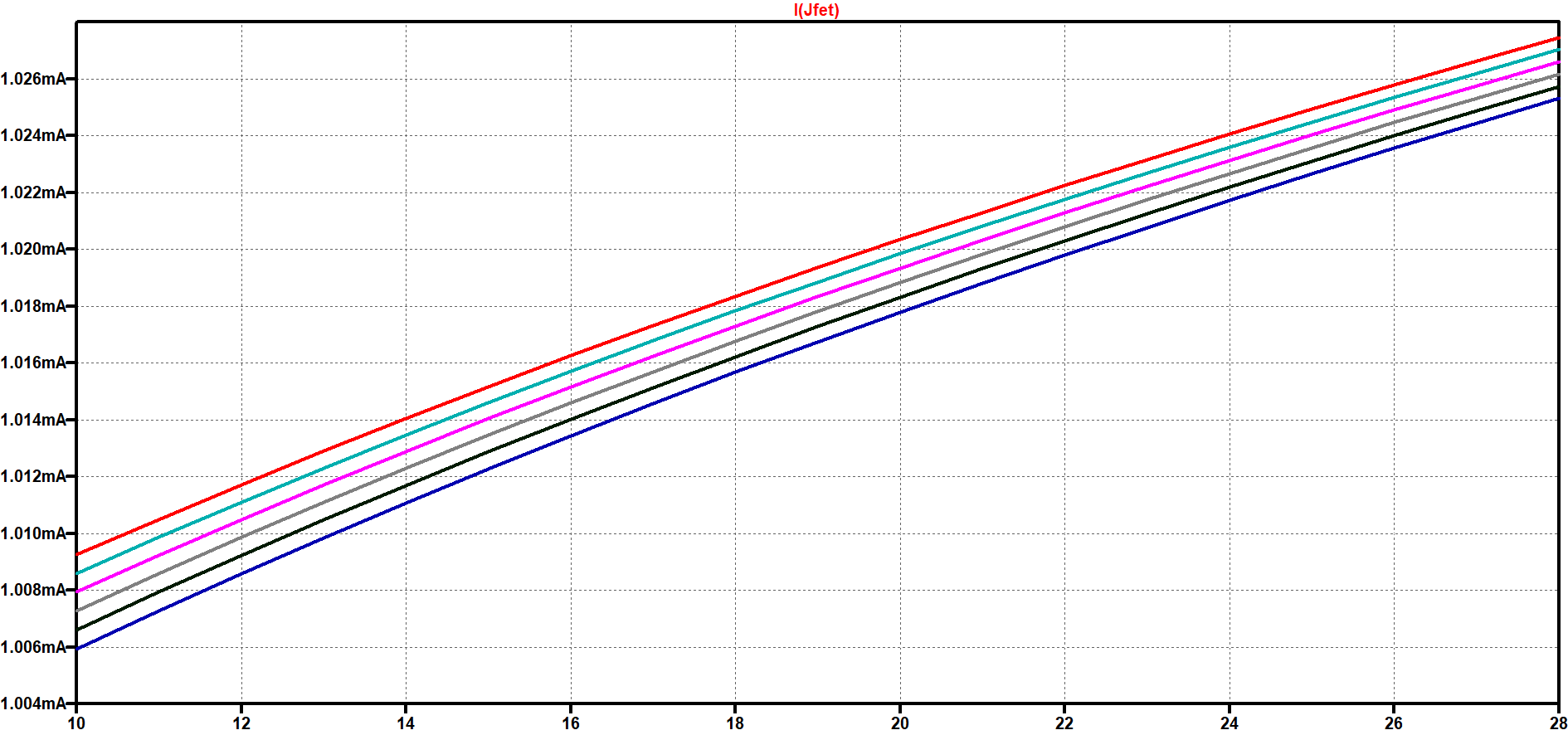
The X-axis of this plot represents the supply voltage swept from 10 V to 28 V. The Y-axis shows the current. Each color line represents a different load resistance.

Howland Current Source

The Howland current source is a voltage controlled current source using a differential feedback architecture. This architecture reduces variation from changes to power supply voltage as well as load resistance.

This implementation requires careful control over the balance of the resistors as any mismatch will result in significant deviations in output current.

Circuit Overview

Figure 6 - Howland Current Source Circuit

Analysis

To analyze this circuit we use Kirchoff’s current rules to perform nodal analysis. Recall that Kirchhoff current law states that the sum of all currents going in and out of a circuit equal zero.

\[\Large \sum I = 0\] Equation 7 - Kirchoff's Current Law

Additionally, the output of an amplifier is the gain of the amplifier, multiplied by the difference between the two terminals.

\[\Large V_o = A \cdot (V_p - V_n)\] Equation 8 - Differential Amplifier Equation

The inverting input of the op-amp can be modelled as a voltage divider from the output of the op-amp.

\[\Large V_n = V_o \cdot \left( \frac{R_1}{R_1 + R_2} \right)\] Equation 9 - Op-Amp Inverting Node Voltage

Moving now to using current analysis - The non-inverting input requires summation of multiple currents.

\[\Large \frac{V_o - V_p}{R_3} + \frac{V_{in}-V_p}{R_4} - \frac{V_p}{R_L} = 0\] Equation 10 - Circuit Current Summation, Non-Inverting Node

That is, the sum of currents through $R_3$, $R_4$, and $R_L$ equal zero. To find the current only through $R_L$ this term can be moved right hand side using algebraic manipulation.

\[\Large \frac{V_o - V_p}{R_3} + \frac{V_{in}-V_p}{R_4} = \frac{V_p}{R_L} = I_o\] Equation 11 - Output Current Derivation

Expand and factor out $V_p$

\[\Large \frac{V_o}{R_3} + \frac{V_{in}}{R_4} = V_p \left( \frac{1}{R_3} + \frac{1}{R_4} + \frac{1}{R_L} \right)\] Equation 12 - Output Current Derivation, Expanded and Factored

Using op-amp properties that $V_p = V_n$ then substitute $V_o$ for the resistance equivalent.

\[\Large V_p = V_n = V_o \cdot \frac{R_1}{R_1 + R_2}\] Equation 13 - Positive Node Equivalence Derivation

Rearrange for $V_p$.

\[\Large V_o = \frac{R_1+R_2}{R_1}\cdot V_p\] Equation 14 - Output Voltage Derivation

Substitute $V_o$ for this value.

\[\Large \frac{\frac{R_1+R_2}{R_1}\cdot V_p}{R_3} + \frac{V_{in}}{R_4} = V_p \left( \frac{1}{R_3} + \frac{1}{R_4} + \frac{1}{R_L} \right)\] Equation 15 - Substituted Intermediate Step

This equation can then be algebraically manipulated, substituting $V_p$ and $V_o$ using the prior equations.

Next, Recall that at balance the resistors are equal.

\[\Large R_1R_3 = R_2 R_4\] Equation 16 - Resistance Equivalence at Balance

Simplification of the prior substituted equation results in the following equation.

\[\Large I_o = V_{in} \cdot \frac{R_1 R_3}{R_1 R_3 R_4 + R_L (R_1 R_3 - R_2 R_4)}\] Equation 17 - Howland Output Current Equation

Knowing that $R_1R_3$ is equivalent to $R_2 R_4$ it can be cancelled from the denominator yielding a simplified equation.

\[\Large I_o = V_{in} \cdot \frac{R_1 R_3}{R_1 R_3 R_4 + R_L \cdot 0} = V_{in} \frac{R_1 R_3}{R_1 R_3 R_4}\] Equation 18 - Simplifying Steps for Output Current Equation at Balance

It can again be simplified one step further by cancelling terms in the numerator and denominator yielding a compact equivalent.

\[\Large I_o = V_{in} \cdot \frac{1}{R_4} = \frac{V_{in}}{R_4}\] Equation 19 - Simplified Output Current Equation at Balance

In summary at balance the relationship is as follows:

\[\Large I_o = \frac{V_{in}}{R_4}\] Equation 20 - Company Simplified Current Equation at Balance

Sensitivity Analysis

Performing partial differentiation of the base equation results in the following equations. Note that the sign provides an intuition as to the behavior. Specifically, Increasing $R_2$ and $V_{in}$ will increase the current, whereas changing all the other inputs will decrease the output current $I_o$.

\[\Large \frac{\partial I_{O}}{\partial R_{1}} = - \frac{R_{2} R_{3} R_{4} R_{L} V_{i}}{\left(R_{1} R_{3} R_{4} + R_{1} R_{3} R_{L} - R_{2} R_{4} R_{L}\right)^{2}}\] Equation 21 - Howland Partial Derivative, Output vs R1 \[\Large \frac{\partial I_{O}}{\partial R_{2}} = \frac{R_{1} R_{3} R_{4} R_{L} V_{i}}{\left(R_{1} R_{3} R_{4} + R_{L} \left(R_{1} R_{3} - R_{2} R_{4}\right)\right)^{2}}\] Equation 22 - Howland Partial Derivative, Output vs R2 \[\Large \frac{\partial I_{O}}{\partial R_{3}} = - \frac{R_{1} R_{2} R_{4} R_{L} V_{i}}{\left(R_{1} R_{3} R_{4} + R_{1} R_{3} R_{L} - R_{2} R_{4} R_{L}\right)^{2}}\] Equation 23 - Howland Partial Derivative, Output vs R3 \[\Large \frac{\partial I_{O}}{\partial R_{4}} = - \frac{R_{1} R_{3} V_{i} \left(R_{1} R_{3} - R_{2} R_{L}\right)}{\left(R_{1} R_{3} R_{4} + R_{L} \left(R_{1} R_{3} - R_{2} R_{4}\right)\right)^{2}}\] Equation 24 - Howland Partial Derivative, Output vs R4 \[\Large \frac{\partial I_{O}}{\partial R_{L}} = - \frac{R_{1} R_{3} V_{i} \left(R_{1} R_{3} - R_{2} R_{4}\right)}{\left(R_{1} R_{3} R_{4} + R_{L} \left(R_{1} R_{3} - R_{2} R_{4}\right)\right)^{2}}\] Equation 25 - Howland Partial Derivative, Output vs Load Resistance \[\Large \frac{\partial I_{O}}{\partial V_{i}} = \frac{R_{1} R_{3}}{R_{1} R_{3} R_{4} + R_{L} \left(R_{1} R_{3} - R_{2} R_{4}\right)}\] Equation 26 - Howland Partial Derivative, Output vs Input Voltage

Design Considerations

Limitations

First, a note on the design limitations. As with a typical operational amplifier there are limits to the compliance voltage as well as the power supply voltage rail margin. The current limit of the device, as well thermal management considerations.

The values must be chosen such that the resistors are not too high such that they impact the biasing condition of the op-amp.

Supply Limits

Operational amplifiers, even rail to rail devices are unable to output exactly the input supply rail. They need some margin to operate. This condition becomes the compliance limit threshold and is a limiting factor in operation.

\[\Large V_{supply} \geq V_o + V_{margin}\]

Current Limit

The operational amplifier cannot output infinite current. Each device has limitations in how much current it can source or sink. For additional current a discrete output stage could be used.

Resistor Trimming

The resistors should be precision. Even 1% mismatch can cause considerable deviation. In this configuration it would be ideal to utilize a mechanism to trim the resistors for optimal matching. Temperature coefficient mismatches can also affect the output current and should be considered for best long term stability.

Thermal Management and Quiescent Power Usage

For low current applications thermal management may not be a concern, but for high current applications thermal management could become a necessity. Recall that power dissipated as heat is proportional to the square of the current and the resistance. The resistors chosen therefore impact both the system thermal performance as well as the quiescent power usage.

\[\Large P_{diss} = I^2 R\]

Compliance Limit

Note that in this particular Howland configuration there is a voltage divider effect with equal resistors. This means that the output to the load will be half the output from $V_o$. This significantly reduces the maximum available compliance voltage from the op-amp.

\[\Large I_o \leq \frac{0.5\cdot V_{o(max)}}{R_L}\]

where $V_{o(max)}$ would be something on the order of $(V_s - V_{margin}) / 2$. Where the margin would be the maximum rail-rail operational headroom required from the op-amp. The factor of 2 accounts for the voltage divider. This factor would change if the resistors were no longer equal.

Additional Considerations

The Howland design needs an operational amplifier with a high common mode rejection ratio, low bias current, and low offset voltages. These will directly impact the system mismatch and should also be considered for critical designs.

Component Value Calculation

Requirement	Symbol	Description
Output Current	$I_o$	Desired maximum output current.
Control Voltage	$V_{in}$	Maximum control voltage to calculate current output.
Allowable Error	$\epsilon_I$	Allowable current error, used to determine required tolerance.
Load Resistance	$R_L$	Maximum load resistance, to determine compliance voltage.

Summary

Figure 7 - SPICE Simulation Schematic Figure 8 - SPICE Simulation Summary, Output vs Input Voltage

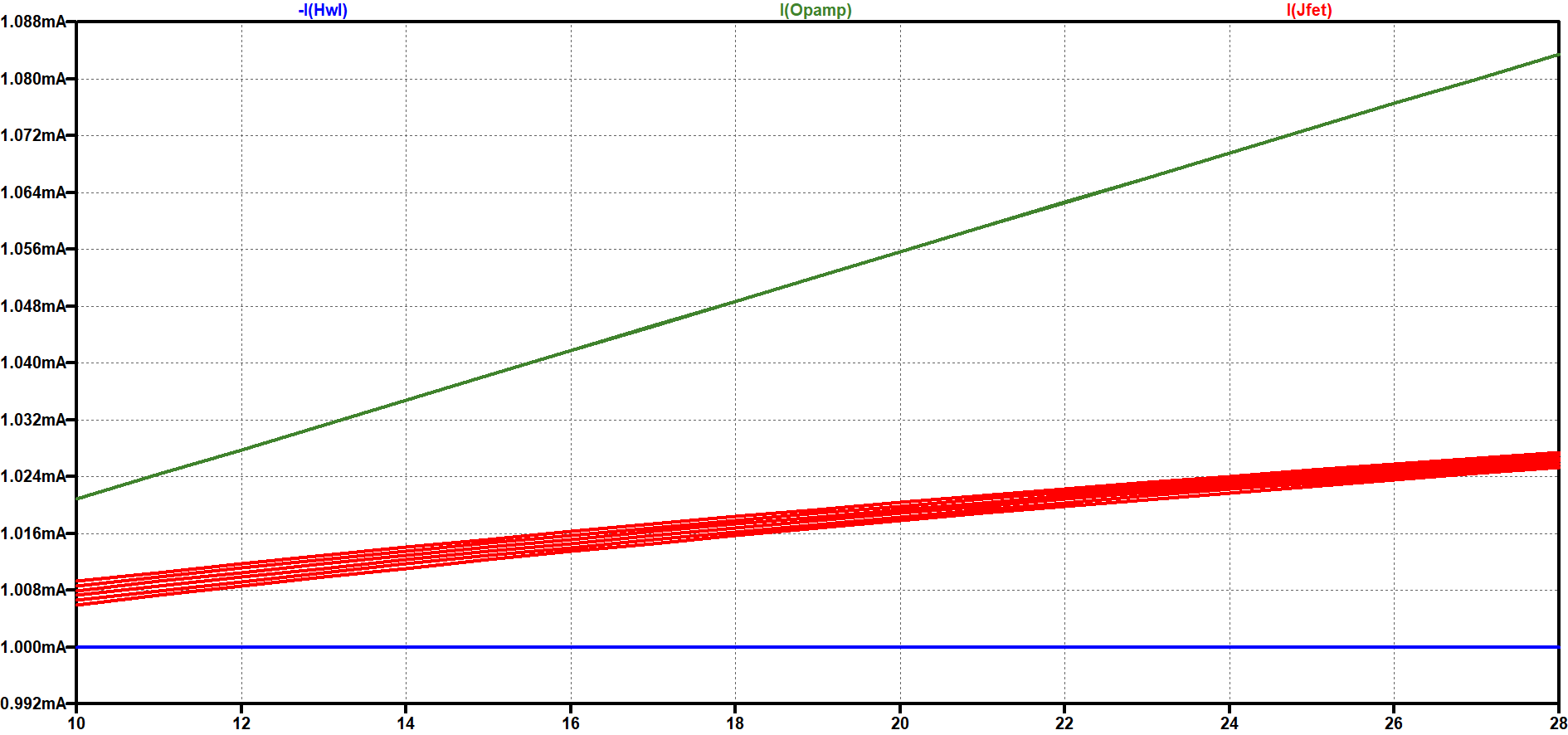
Three current source architectures were simulated with a $1mA$ current target. The JFET was the simplest to implement utilizing only two components. The JFET suffers from variation due to the intrinsic channel length modulation characteristics of the device as well as slightly due to the load resistance. The Op-Amp produces nearly no variation due to change in load, however suffers the most from change in supplied voltage. Ultimately the Howland under ideal conditions performs the best with near zero change in output current with a change in applied voltage or variation in load resistors over the chosen range.

>>Download Simulation File<<

Definitions

Term	Description
CMRR	Common Mode Rejection Ratio
JFET	Junction Field Effect Transistor
Op-Amp	Operation Amplifier
MOSFET	Metal Oxide Semiconductor Field Effect Transistor

References

Reference	Description
AN-1515 A Comprehensive Study of the Howland Current Pump	Technical whitepaper detailing the operational details of the Howland current pump.
Wikipedia - Constant Current Diode	Additional details of the constant current diode.
Georgia Tech - The JFET	Explanation of JFET with formulas.
LTspice	SPICE Circuit Simulator

Table of Figures

1. LTSpice Simulation Schematic
2. JFET Semiconductor Structure
3. JFET Load Resistance Sensitivity Plot
4. JFET Simulation Circuit
5. JFET Simulation Results, Current vs Applied Voltage
6. Howland Current Source Circuit
7. SPICE Simulation Schematic
8. SPICE Simulation Summary, Output vs Input Voltage

Table of Equations

1. JFET Gate Source Voltage
2. JFET Drain Resistance
3. Drain Current
4. Drain Saturation
5. JFET Drain Current
6. JFET Drain Current vs Load Resistance Derivative
7. Kirchoff’s Current Law
8. Differential Amplifier Equation
9. Op-Amp Inverting Node Voltage
10. Circuit Current Summation, Non-Inverting Node
11. Output Current Derivation
12. Output Current Derivation, Expanded and Factored
13. Positive Node Equivalence Derivation
14. Output Voltage Derivation
15. Substituted Intermediate Step
16. Resistance Equivalence at Balance
17. Howland Output Current Equation
18. Simplifying Steps for Output Current Equation at Balance
19. Simplified Output Current Equation at Balance
20. Company Simplified Current Equation at Balance
21. Howland Partial Derivative, Output vs R1
22. Howland Partial Derivative, Output vs R2
23. Howland Partial Derivative, Output vs R3
24. Howland Partial Derivative, Output vs R4
25. Howland Partial Derivative, Output vs Load Resistance
26. Howland Partial Derivative, Output vs Input Voltage