Pistachio Gravimetric Analysis

Table of Contents

1. Introduction
2. The Experiment
3. Measurements
4. Results
5. Additional Factors Considered
6. Conclusion
7. Raw Data
8. Table of Figures

Introduction

Have you ever wondered whether buying pistachios with shells or without shells offers the better value? For example here, there are $1360g$ of pistachios with shells offered for $\$ 16$, or $680g$ without shells for $\$18$.

This article presents an experiment in which a sample from a bag of pistachios with shells was processed nut by nut, with the mass of each kernel and shell measured separately to determine not only the mass distribution of the combined sample but the ratio of nut to shell as well.

The Experiment

For this experiment, a randomly selected bowl of pistachios was prepared from a freshly purchased bag bearing an expiration date of 30 July 2026, a lot number of $2531152754101$, and a vendor number of $74932$.

Each nut had the kernel extracted by hand, then the shell weighted followed by the kernel by an Ohaus electronic balance. These samples were separated into pre-weighted storage containers for obtaining total mass.

Measurements

Figure 1 - Textual Interface

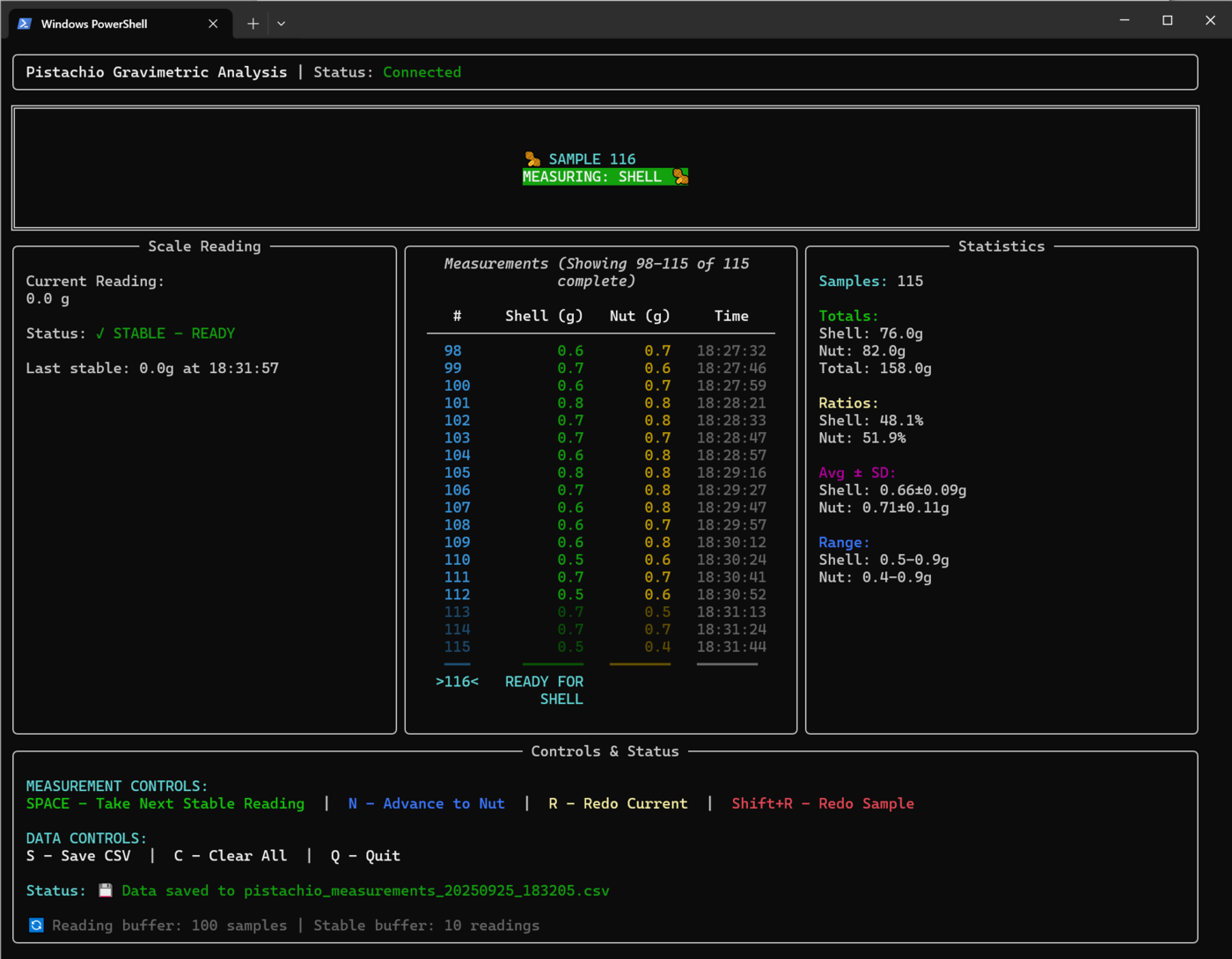
A total of 115 paired measurements were collected and recorded using a custom Python-Textual application connected to the Ohaus electronic balance via a custom USB to Serial converter. The resulting histograms and distribution charts are shown below.

Any fragments that separated during shelling were discarded and not included in the measurements.

Figure 2 - Measurement Results - Nut Histogram

Figure 3 - Measurement Results - Shell Histogram

Figure 4 - Measurement Results - Nut Mass

Figure 5 - Measurement Results - Shell Mass

Figure 6 - Measurement Results - Combined Nut and Shell Histogram

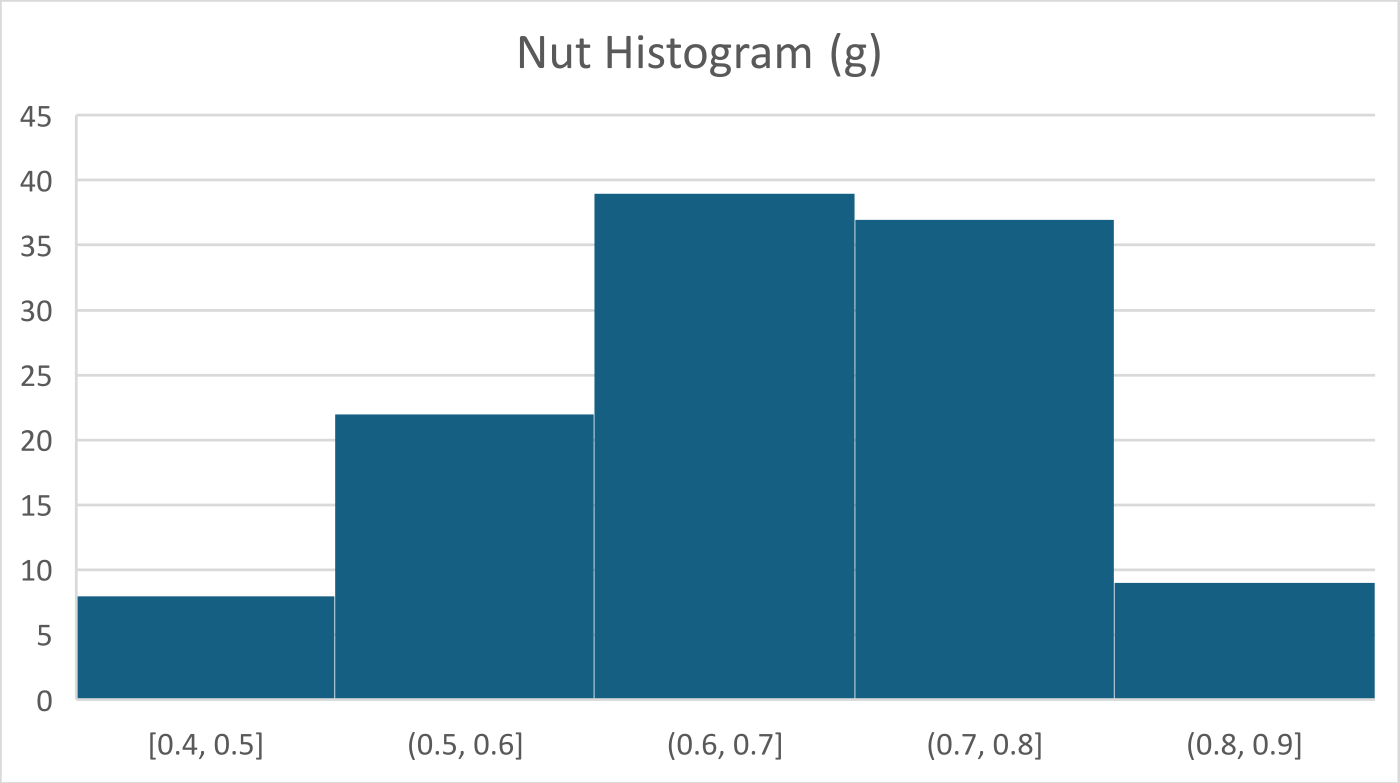
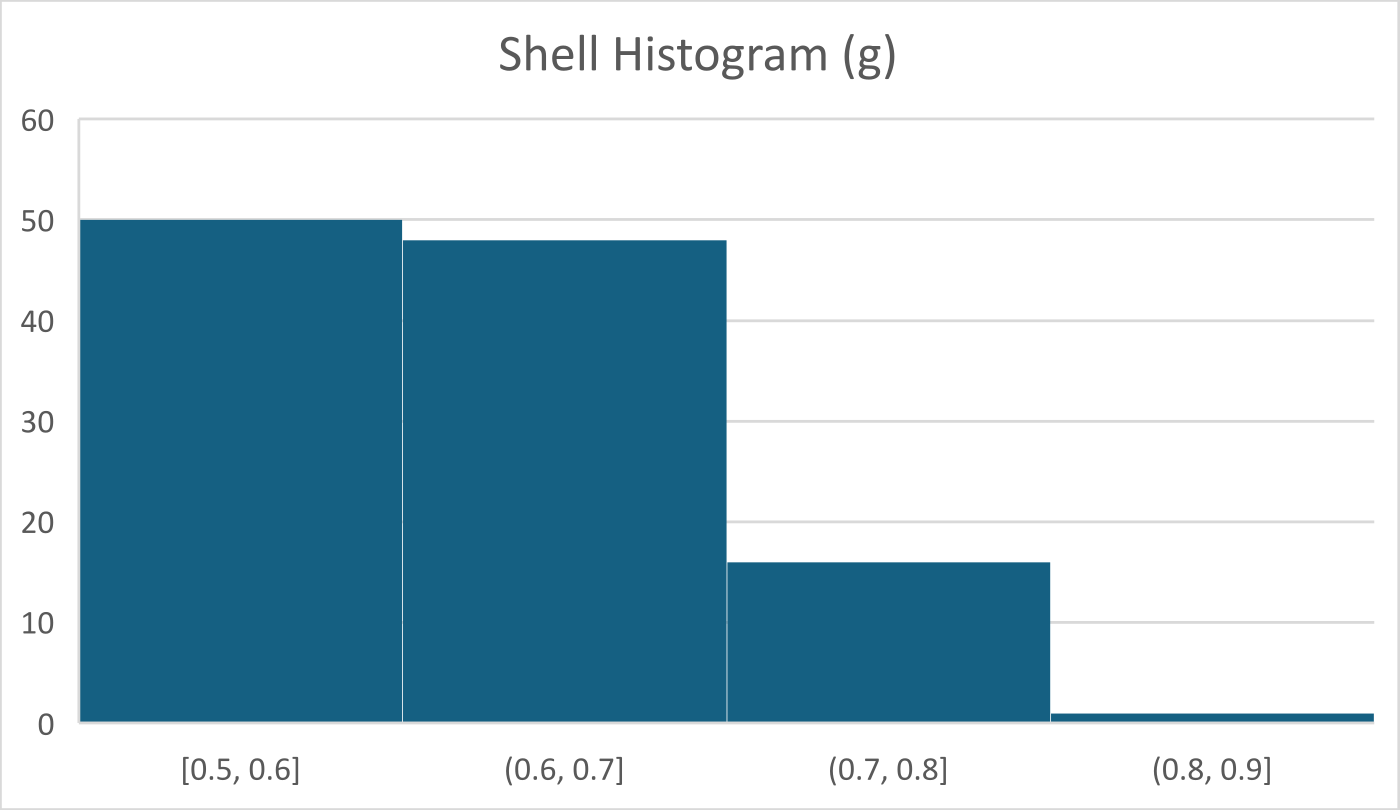
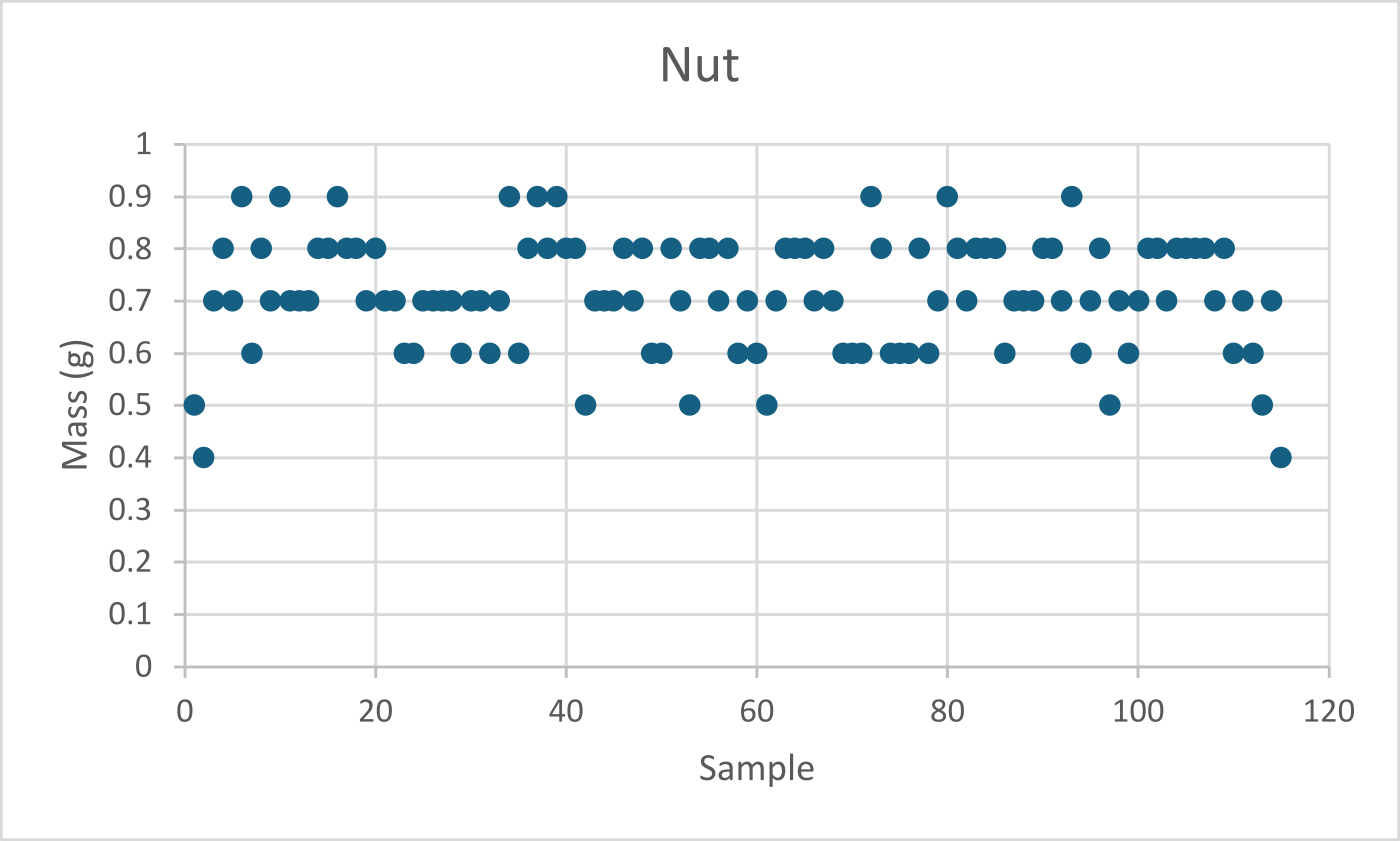
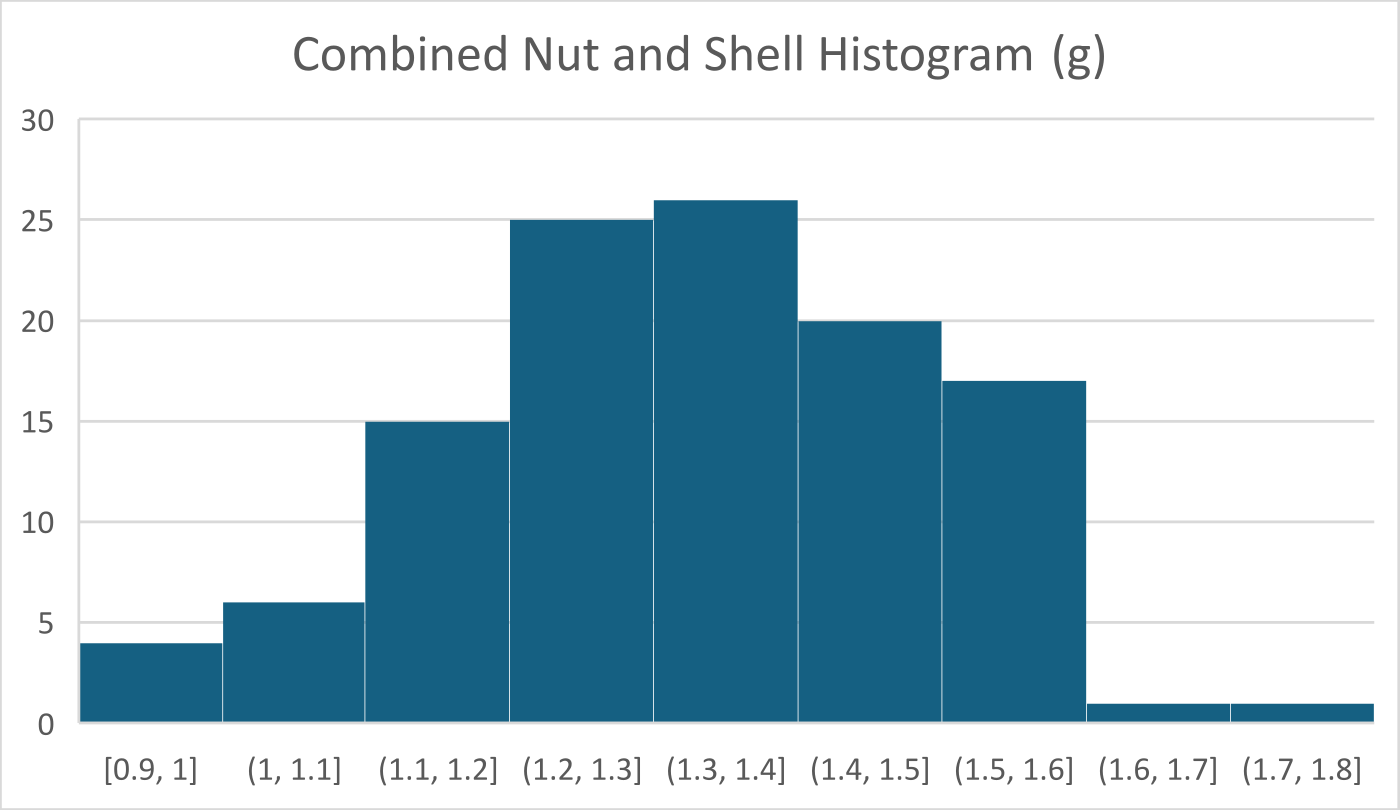
Results

The results indicate that, on average, pistachio kernels represent approximately $51.6\%$ of the total measured mass.

\[\Large r = \frac{net}{tot}\]

Parameter	Value
With Shells ($1360g$)	$16
Without Shells ($680g$)	$18

Assuming the population remains constant for all bags then the estimated grams per dollar is as follows:

Parameter	Value
Mass per dollar without shell	$37.78g/$$
Mass per dollar with shell	$43.86g/$$

\[\Large \frac{1360g \cdot51.6\%}{$16} = 43.86g/$\]

In practical terms, pistachios with shells provide more edible mass per dollar. However, if convenience and time are important, the shelled variety may be the more realistic choice despite the increased cost.

Additional Factors Considered

Figure 7 - Measurement Results - Combined Nut and Shell Mass

Parameter	Value	Units
Shell Container Tare Mass	24.7	g
Nut Container Tare Mass	24.7	g
Weight Boat Mass	14.0	g
Filled Container Mass, Nuts	106.1	g
Filled Container Mass, Shells	101.2	g

Several factors may influence these results. The electronic balance had a resolution of 0.1g, which introduces a potential margin of error. This limitation was mitigated by combining all samples in their respective bins for a final total mass measurement, which improved the accuracy of the calculated ratios.

In some cases, thin pistachio skins detached during handling. These were excluded from both nut and shell weights and discarded, as for this analysis they would be considered part of the inedible fraction (“shell”).

Conclusion

This experiment demonstrates that pistachios with shells yield a greater edible mass per dollar compared to their pre-shelled counterparts, with kernels accounting for slightly more than half of the total mass. While shelled pistachios offer convenience, unshelled pistachios provide better value—and perhaps a small measure of entertainment in the process.

Beyond the practical findings, this project highlights how simple measurements and analysis can uncover useful insights, and it raises interesting questions about the commercial processing and sorting of pistachios – are they sorted systematically by size and mass, or does nature account for their consistent distribution?

Raw Data

Shell	Nut
0.5	0.5
0.5	0.4
0.6	0.7
0.7	0.8
0.7	0.7
0.7	0.9
0.6	0.6
0.6	0.8
0.6	0.7
0.7	0.9
0.6	0.7
0.6	0.7
0.6	0.7
0.6	0.8
0.7	0.8
0.8	0.9
0.7	0.8
0.8	0.8
0.8	0.7
0.8	0.8
0.7	0.7
0.6	0.7
0.7	0.6
0.6	0.6
0.7	0.7
0.7	0.7
0.7	0.7
0.7	0.7
0.7	0.6
0.7	0.7
0.6	0.7
0.6	0.6
0.7	0.7
0.9	0.9
0.6	0.6
0.7	0.8
0.7	0.9
0.8	0.8
0.7	0.9
0.5	0.8
0.6	0.8
0.7	0.5
0.6	0.7
0.7	0.7
0.7	0.7
0.7	0.8
0.5	0.7
0.5	0.8
0.5	0.6
0.7	0.6
0.8	0.8
0.5	0.7
0.5	0.5
0.8	0.8
0.8	0.8
0.6	0.7
0.7	0.8
0.5	0.6
0.6	0.7
0.6	0.6
0.6	0.5
0.7	0.7
0.8	0.8
0.8	0.8
0.6	0.8
0.6	0.7
0.7	0.8
0.7	0.7
0.6	0.6
0.6	0.6
0.8	0.6
0.6	0.9
0.8	0.8
0.7	0.6
0.5	0.6
0.6	0.6
0.7	0.8
0.6	0.6
0.6	0.7
0.7	0.9
0.6	0.8
0.8	0.7
0.7	0.8
0.7	0.8
0.7	0.8
0.6	0.6
0.6	0.7
0.6	0.7
0.8	0.7
0.7	0.8
0.7	0.8
0.7	0.7
0.7	0.9
0.7	0.6
0.7	0.7
0.7	0.8
0.7	0.5
0.6	0.7
0.7	0.6
0.6	0.7
0.8	0.8
0.7	0.8
0.7	0.7
0.6	0.8
0.8	0.8
0.7	0.8
0.6	0.8
0.6	0.7
0.6	0.8
0.5	0.6
0.7	0.7
0.5	0.6
0.7	0.5
0.7	0.7
0.5	0.4

Table of Figures

1. Textual Interface
2. Measurement Results - Nut Histogram
3. Measurement Results - Shell Histogram
4. Measurement Results - Nut Mass
5. Measurement Results - Shell Mass
6. Measurement Results - Combined Nut and Shell Histogram
7. Measurement Results - Combined Nut and Shell Mass